From: Bayesian Models for Astrophysical Data, Cambridge Univ. Press

(c) 2017,  Joseph M. Hilbe, Rafael S. de Souza and Emille E. O. Ishida  

 

you are kindly asked to include the complete citation if you used this material in a publication

​

​

Code 6.7: Bayesian Poisson model using pymc3

====================================================

import numpy as np
import pandas
import pylab as plt
import pymc3 as pm

from scipy.stats import norm, binom, poisson

​

# Data
np.random.seed(18472)                                              # set seed to replicate example
nobs= 750                                                                   # number of obs in model 

​

x1_2 = binom.rvs(1, 0.7, size=nobs)
x2 = norm.rvs(loc=0, scale=1.0, size=nobs)

xb = 1 - 1.5 * x1_2  - 3.5 * x2                                    # linear predictor           
exb = np.exp(xb)
py = poisson.rvs(exb)                                                 # create y as adjusted

​

df = pandas.DataFrame({'x1_2': x1_2, 'x2':x2, 'py': py})                  # re-write data

​

# Fit
niter = 10000                                                             # parameters for MCMC

​

with pm.Model() as model_glm:
    # define priors
    beta0 = pm.Flat('beta0')
    beta1 = pm.Flat('beta1')
    beta2 = pm.Flat('beta2')

​

    # define likelihood
    mu = np.exp(beta0 + beta1*x1_2 + beta2 * x2)
    y_obs = pm.Poisson('y_obs', mu, observed=py)

​

    # inference
    start = pm.find_MAP()                                       # Find starting value by optimization
    step = pm.NUTS()
    trace = pm.sample(niter, step, start, progressbar=True)

​

# Output
pm.summary(trace)

​

# show graphical output
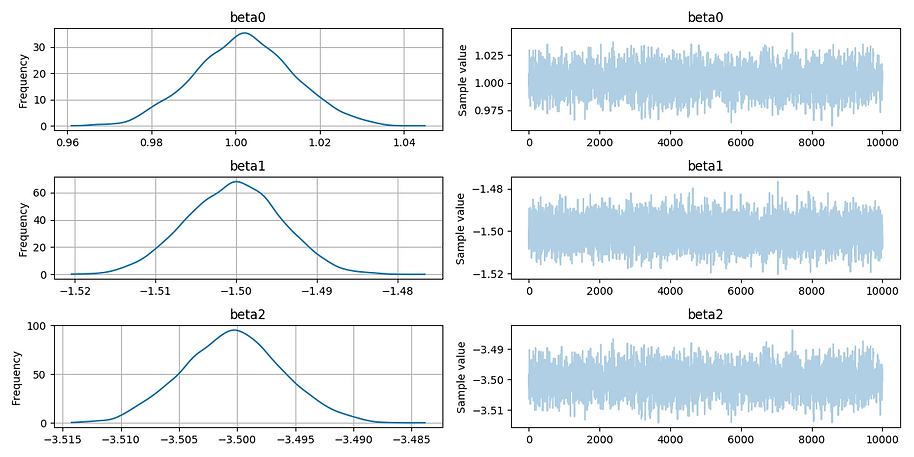
pm.traceplot(trace)
plt.show()

====================================================